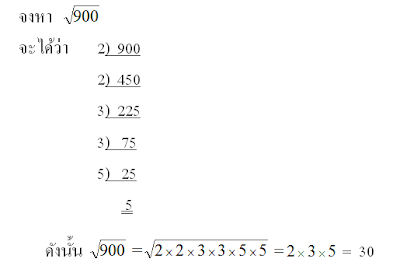การหากรณฑ์ที่สองโดยการหารยาว
การหากรณฑ์ที่สองหรือค่าหลักรากที่สองของจำนวนจริงบวกใดๆ โดยปกติแล้วถ้าเป็นการหากรณฑ์ที่สองของจำนวนจริงบวกที่ถอดรากได้ลงตัวจะสามารถทำได้โดยง่าย ดังนี้
หรือถ้าจำนวนจริงบวกมีค่ามากก็อาจจะหากรณฑ์ที่สองได้โดยการหารสั้น เช่น
แต่ถ้ากรณฑ์ที่สองของจำนวนจริงที่อยู่ในรูปติดกรณฑ์ซึ่งคำตอบจะเป็นทศนิยม เราสามารถหากรณฑ์ที่สองได้โดยการตั้งหารยาว ซึ่งมีวิธีการดังนี้

ขั้นที่ 1 แบ่งตัวเลขออกเป็นกลุ่ม ๆ ละ 2 จำนวน โดยให้ทศนิยมเป็นจุดเริ่ม แบ่งไปทั้งทางซ้ายและทางขวาของจุดทศนิยม
215 = 215.0000
215 แบ่งได้เป็น 2 15 . 00 00
เขียนในรูปการหารยาวได้ดังนี้
ขั้นที่ 2 หาจำนวนที่ยกกำลังสองแล้วได้ค่ามากที่สุดและมีค่าไม่เกินตัวเลขกลุ่มแรก (นับลำดับของกลุ่มจากซ้ายไปขวา) นำกำลังสองของจำนวนนั้นมาลบออกจากตัวเลขกลุ่มแรก
ในที่นี้คือหาจำนวนที่ยกกำลังสองแล้วมีค่ามากที่สุดและไม่เกิน 2
นั่นคือ 12 = 1 ใช้ได้
22 = 4 ใช้ไม่ได้ เนื่องจากมีค่าเกิน 2
นำมาเขียนหารยาวได้เป็น
ขั้นที่ 3 ดึงตัวเลขกลุ่มที่สองลงมา จากนั้นนำ 2 มาคูณกับผลหารที่ได้ในขั้นที่ 2 แล้วหาตัวเลขมาต่อท้ายค่าที่ได้แล้วทำให้ผลคูณของตัวเลขนั้นกับค่าดังกล่าวมีค่าไม่เกินตัวตั้ง
ขั้นที่ 4 ดึงตัวเลขกลุ่มถัดมาลงมา แล้วทำแบบเดียวกับขั้นที่ 3 ทำไปเรื่อย ๆ จนกระทั้งผลหารถึงทศนิยมตำแหน่งที่สาม
การหากรณฑ์ที่สองด้วยวิธีนี้เริ่มต้นอาจจะค่อนข้างสับสนในการหาคำตอบ เมื่อได้ลองฝึกทำบ่อยๆ จะเกิดความชำนาญและทำให้รู้สึกว่าเป็นวิธีที่ง่ายและไม่ยากเลย
ผู้เขียน : นางสาวปิยาภรณ์ เขียวหวาน นักศึกษาปริญญาโท
สาขาวิชาคณิตศาสตรศึกษา รุ่นที่ 5 เลขที่ 14
มหาวิทยาลัยราชภัฏอุบลราชธานี
มหาวิทยาลัยราชภัฏอุบลราชธานี